Упрощенные методы моделирования полипептидов
Во многих случаях для ускорения расчетов используются сильно упрощенные модели белка, когда каждая аминокислота рассматривается как одна или две сферы. Для того, чтобы придать такому модельному полимеру свойства белка, используются специально подобранные функции энергии или, например, сферам приписывают заряды, характерные для аминокислот. Расчеты также значительно упрощаются, если предполагается, что сферы, соответствующие аминокислотам, находятся в вершинах решетки.
Модель белка, основанная на предположении о том, что его аминокислотные остатки находятся в вершинах двумерной решетки, наверное, является самой приближенной и нереалистичной моделью. Однако, такая модель все же иногда используется из-за простоты и из-за того, что на двумерной решетке число всех возможных конформаций невелико, и поэтому их можно перебрать за разумное время.
Более реалистичными, по сравнению с двумерными, являются трехмерные решетки.
В решеточных моделях взаимодействуют лишь те сферы, которые находятся в соседних вершинах решетки. Так, например, на рисунке изображена упрощенная решеточная модель полипептида, состоящего из 27 мономерных звеньев. Полная энергия конформации (т.е. заданного расположения мономеров в узлах решетки) рассчитывается как сумма контактных взаимодействий:
где 
= 1, если
мономеры i и j валентно не связаны и
находятся в соседних узлах решетки
и 
= 0 в противном случае, 
-
случайная величина с данным
значением среднего и дисперсии.
Траектория сворачивания такого модельного полипептида начинауеся со случайной конформации и рассчитывается при помощи метода Монте-Карло с использованием критерия Метрополиса. Конечная конформация считается нативной. Компьютерные эксперименты проводятся многократно для усреднения результатов.
Динамика моделируемого белка сильно зависит от того, могут ли некоторые узлы решетки оставаться свободными, или же все они должны быть заняты сферами-аминокислотами. В зависимости от этого могут значительно изменяться времена релаксации, совершенно другими становятся и конечные конформации.
Также большое значение имеет неоднородность мономеров в полипептиде - наличие гидрофобных, гидрофильных и нейтральных аминокислотных остатков. В одних работах параметры их взаимодействий выбираются более или менее случайно, в других они связаны со свойствами реальных аминокислот.
В последнем
случае возникает также проблема
решеточной аппроксимации данной
трехмерной структуры белка.
Построение такой аппроксимации
может осуществляться методом
последовательных приближений.
Сначала задается стартовая
структура на решетке, затем эта
структура уточняется сочетанием
движений отдельных звеньев и малых
поворотов молекулы как целого так,
чтобы минимизировать функцию
ошибок - сумму квадратов отклонений
координат атомов на решетке от
координат атомов нативной
структуры. При этом получается локальная минимизация
функции ошибок. Часто
используется метод
глобальной минимизации функции
ошибок при заданной ориентации
решетки относительно белка.
Основной недостаток этого метода
заключается в том, что он, в общем
случае, не гарантирует построение
решеточной аппроксимации без
самопересечения (т.е. не
гарантируется, что в каждом узле
решетки будет не более одного
аминокислотного остатка). Качество
аппроксимации существенно
повышается при отказе от жесткой
фиксации длины межзвенной связи. В
этом случае энергия взаимодействия
соседних звеньев вычисляется так: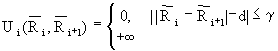 
где d - стандартное расстояние между звеньями решетки, g - порог деформации межзвенной связи.
На рисунке изображена решеточноя модель с простой кубической решеткой. Виртуальные углы в этом случае могут принимать значения 90 0 и 180 0 , а виртуальные торсионные углы - 0 0 , 90 0 ,180 0 и 270 0 . В решеточной модели BCC (body-centered cubic lattice) в центре единичного кубика решетки имеется дополнительный узел. В результате появляется еще два валентных и восемь торсионных углов. Наиболее сложной является решетка FCC (face-centered cubic lattice) - в ней имеются дополнительные узлы в середине каждой грани, что обеспечивает четыре дополнительных валентных угла и шестнадцать торсионных углов.
Довольно часто
используются также и "210
решетки". В них последовательные
звенья соединены между собой
векторами вида 
.
Метод ограничения объема позволяет генерировать все конформации на решетке в объеме, ограниченном известным объемом индивидуального белка. При этом нативные структуры для коротких белков всегда находятся среди лучших по энергии 2% сгенерированных конформаций. Поэтому данный способ иногда применяется для предсказания возможной третичной структуры белка.
Литература: