Метод нормальных мод

Медленные коллективные движения многих атомов играют важную роль в функционировании белков. Традиционный способ теоретического изучения коллективных движений в белках состоит в проведении анализа нормальных мод.

Нориальные моды колебаний являются простыми гармоническими колебаниями около локального энергетического минимума, характеризующегося структурой системы и её энергетическим минимумом . В случае гармонических колебаний , любые возможные варианты могут быть выражены через суперпозицию нормальных мод. В случае ангармоничности , потенциал в районе минимума также может быть хорошо аппроксимирован гармоническим потенциалом и любые малоамплитудные движения могут быть хорошо описаны суммой нормальных мод. Иными словами, при достаточно низких температурах, любая классическая система ведёт себя гармонически. В обычном анализе нормальных мод, характерные колебания энергетически минимизированной системы ( К) и отвечающие им частоты определяются гармоническим потенциалом для всех степеней свободы. Нормальные моды рассчитываются гораздо быстрее, нежели молекулярная динамика, но требуют больших ресурсов памяти.

Спектр нормальных мод трёхмерной системы из N атомов содержит 3N-6 нормальных мод (3N-5 для линейной молекулы). Число мод вычисляется как общее число степеней свободы системы минус число степеней свободы, отвечающих за движение системы как целого (вращение или перемещение). Каждая мода определяется собственным вектором и собственной частотой . Собственный вектор содержит амплитуду и направление движения для каждого атома. Например, в моде i все атомы колеблются с одинаковой частотой .

В макромолекулах низкочастотные моды отвечают коллективным движениям больших атомных групп (например доменов в белках) с одинаковой амплитудой. Более высокочастотные моды локализованы и отвечают колебаниям нескольих или пары атомов (например валентные колебания между атомами углерода и водорода).

С механической точки зрения низкочастотные моды могут быть использованы для определения направлений, вдоль которых молекула наиболее легко деформируется, т.е. для изучения гибкости молекулы. Полученный в гармоническом анализе спектр можно непосредственно сравнивать с экспериментально получаемыми колебательными спектрами.

Силовые константы колебаний в методе нормальных мод определяются как собственные значения матрицы вторых производных потенциальной энергии, вычисленных в равновесном положении. Для высокочастотных колебаний необходим также учет ангармоничности. Метод нормальных мод применяется как к белкам, так и к модельным участкам их вторичной структуры.

Для определения анизотропности движения атома из траектории молекулярной динамики вычисляется матрица:

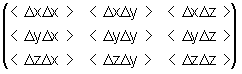
где D x, D y, D z - изменения координат атома за время D t, усреднение производится по времени. Систему координат вращают таким образом, чтобы матрица стала диагональной. Каждый из диагональных элементов такой матрицы - среднее значение квадрата отклонения от среднего положения вдоль соответствующей оси.

Литература:

1. Peraha D., Levy R.M., Karplus M. Motions of an a-helical polypeptide: comparison of molecular and harmonic dynamics. Biopolymers, V. 29, P. 645-677, 1990.
2. McCammon J.A. Protein dynamics. Rep. Prog. Phys., V. 47, P. 1-46, 1984.

<< Назад || Вперёд >>

Обратно в оглавление