Расчёт ньютоновских траекторий движения.
В методе молекулярной динамики
рассчитываются классические (ньютоновские)
траектории движения атомов макромолекулы в
силовом поле эмпирического атом-атомного
потенциала, т. е. моделируется детальная
микроскопическая картина внутренней тепловой
подвижности макромолекулы в субнаносекундных
интервалах времен. Основу метода составляет
численное решение классических уравнений
Ньютона для системы взаимодействующих частиц:
где 
-
радиус-вектор i-го атома, 
- его
масса, 
суммарная сила, действующая на i-ый
атом со стороны остальных частиц: 
Здесь: 
-потенциальная
энергия, зависящая от взаимного расположения
всех атомов; n - число атомов.
Задав координаты и скорости
всех частиц в начальный момент времени, числено
решают уравнения движения, вычисляя на каждом
шаге все силы и новые координаты и скорости
частиц. Температура определяется как средняя
кинетическая энергия, приходящаяся на одну
степень свободы системы:
Здесь N - полное число степеней
свободы молекулы, 
- постоянная
Больцмана. В случае изолированной системы N=3n-6,
поскольку сохраняется ее полный импульс и момент
импульса. Кроме того, в этом случае сохраняется
полная энергия системы, а температура получается
усреднением ее мгновенных значений T(t) по
некоторому интервалу времени.
Потенциальная энергия молекулы задается в виде:
+
+
+
+
+
+
где слагаемые отвечают следующим типам взаимодействий:
- химическим связям; -
валентным углам; 
- торсионным углам; 
- плоским группам; - ван-дер-ваальсовым
контактам; - электростатике;
- водородным связям. Основные типы
структурных взаимодействий представлены на
рисунке:
Указанные слагаемые
имеют различный функциональный вид. Валентные
длины поддерживаются за счет потенциала:
где суммирование проводится по
всем химическим связям, 
-
обозначение для равновесных валентных длин, r -
текущие длины связей, 
- соответствующие
силовые константы (посмотреть
валентные колебания). Уравнение, описывающее
потенциал валентных связей следует из закона
Гука. Это уравнение параболы:
Валентные углы задаются
потенциалами
где 
- равновесные
значения углов, 
- их текущие значения, 
- силовые константы (посмотреть
колебания валентного угла). Уравнение,
описывающее потенциал валентных связей также
следует из закона Гука. Это уравнение параболы:
Энергия торсионных взаимодействий и потенциалов, отвечающих плоским группам, записываются в одинаковом виде:
где n - кратность торсионного
барьера, 
- сдвиг фазы, константы 
определяют высоты потенциальных барьеров
двугранных углов 
(посмотреть вращение
торсионного угла). Энергия торсионных углов
может быть задана с помощью простой
периодической функции, как это показано на
рисунке:
Ван-дер-ваальсовые
взаимодействия атомов, разделенных тремя и более
валентными связями описываются с помощью
потенциалов Леннард-Джонса: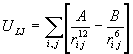
Параметры потенциала A и B зависят от
типов атомов i и j, участвующих во взаимодействии; 
- расстояние
между этими атомами. Аналитический вид
такого потенциала представлен на рисунке:
Очевидно, что вид потенциала зависит от свойств атомов, участвующих в образовании Ван-дер-Ваальсовых связей. Ниже, на рисунке представлен вид потенциала для разных пар атомов:
Электростатические взаимодействия
задаются кулоновским потенциалом
где 
, 
- парциальные заряды на атомах, 
- диэлектрическая проницаемость среды.
Водородные связи возникают и
исчезают в процессе движения атомов между теми
из них, которые имеют донорно-акцепторный статус.
Функциональный вид потенциала водородной связи
аналогичен потенциалу ван-дер-ваальсовым
взаимодействий: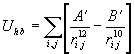
Существуют различные наборы параметров для потенциалов взаимодействий. Их значения определяются из учета различных типов экспериментальных данных (спектральные, калориметрические, кристаллографические) и квантовомеханических расчетов.
Литература: