Методы ускорения расчётов молекулярной динамики.
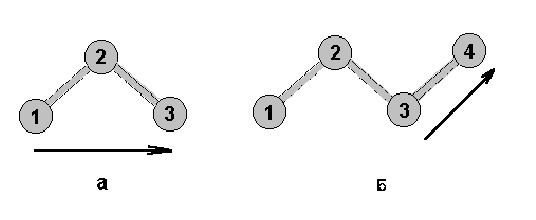
Время, необходимое для расчета траектории молекулы, можно значительно сократить, уменьшая число степеней свободы. Существует два способа ограничения движений длин валентных связей и углов. В одном случае длины валентных связей и значения валентных углов жестко фиксированы, в другом случае на них накладываются упругие ограничения с очень большой константой упругости. Статистические свойства жестко и упруго ограниченных систем, вообще говоря, различны. При разных формах упругого потенциала получаются статистически разные результаты, один из таких потенциалов соответствует жестко фиксированным валентным связям и углам. При этом, в общем случае, упругие потенциалы статистически предпочтительнее как для валентных связей, так и для валентных углов. Рассмотрим, например, следующий численный эксперимент: с помощью метода молекулярной динамики моделировали движение трехатомной (рис., а) и четырехатомной молекул (рис., б) в растворе со сферическими молекулами. Оказалось, что в случае жестких ограничений, в отличие от упругих, вектора, соединяющие первый и третий атомы в случае (а) и первый и четвертый атомы в случае (б), неравномерно распределены по сфере:

Последние исследования в этой
области показали, что колебания валентных
углов, по-видимому, связаны с
коллективными движениями в
молекуле и, из-за плотной упаковки
атомов внутри белка небольшие
флуктуации валентных углов (![]() )
играют существенную роль в
движениях, включающих другие
степени свободы. При фиксации
валентных углов амплитуда
флуктуаций торсионных углов
уменьшается в 2 раза, а
конформационные переходы по
торсионным углам из одного
минимума энергии в другой исчезают
совсем.
)
играют существенную роль в
движениях, включающих другие
степени свободы. При фиксации
валентных углов амплитуда
флуктуаций торсионных углов
уменьшается в 2 раза, а
конформационные переходы по
торсионным углам из одного
минимума энергии в другой исчезают
совсем.
В некоторых случаях степени свободы, соответствующие изменениям значений валентных углов, учитываются неявно. Этот учет валентных углов незначительно увеличивает время счета, но значительно увеличивает конформационную подвижность, благодаря чему полученные результаты в большей степени соответствуют экспериментальным данным.
Иногда используют алгоритмы, в которых переменные, соответствующие медленным степеням свободы, постоянны на протяжении некоторого числа шагов. Однако, при таких расчетах происходит довольно быстрое накопление ошибки. Этого недостатка лишены методы MTS (multiple-time-step methods). В этих методах для вычисления сил, соответствующих быстрым и медленным степеням свободы, используются разные временные интервалы. Время счета при этом сокращается в 4 - 5 раз.
Как правило, в
методе молекулярной динамике для
ускорения расчетов
ван-дер-ваальсовые, водородные и
электростатические взаимодействия
рассчитываются только между
атомами, находящимися на
расстоянии меньшем, чем радиус
обрезания (10-15![]() ). Недавно был предложен метод PPPC (particle-particle and
particle-cell) расчета кулоновских
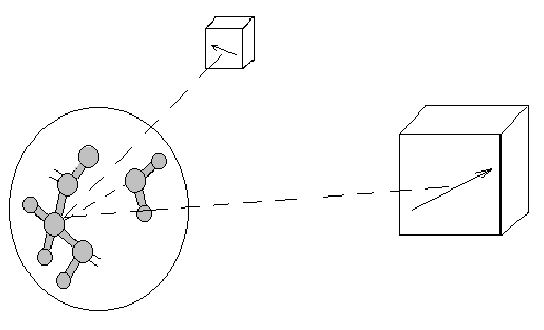
взаимодействий. В методе РРРС
каждый атом взаимодействует с
ближними атомами путем обычных
кулоновских взаимодействий, а с
далеко отстоящими ячейками через
общий заряд и дипольный момент этой
ячейки. Размеры ячеек возрастают
как функции расстояния от атома:
). Недавно был предложен метод PPPC (particle-particle and
particle-cell) расчета кулоновских
взаимодействий. В методе РРРС
каждый атом взаимодействует с
ближними атомами путем обычных
кулоновских взаимодействий, а с
далеко отстоящими ячейками через
общий заряд и дипольный момент этой
ячейки. Размеры ячеек возрастают
как функции расстояния от атома:
Литература: