МАТЕМАТИЧЕСКИЕ МОДЕЛИ ДЛЯ ОЦЕНКИ ЭНТРОПИЙ ОБРАЗОВАНИЯ ПЕРЕХОДНЫХ СОСТОЯНИЙ МОЛЕКУЛ И ПРОМЕЖУТОЧНЫХ МОЛЕКУЛЯРНЫХ КОМПЛЕКСОВ В ГАЗОВОЙ ФАЗЕ ПО ТЕРМОДИНАМИЧЕСКИМ ДАННЫМ

Дудоров В.В., Мельчакова Т.А., Гурбатова А.П.

(Н.Новгород)

В основу предлагаемых моделей заложено представление о двухстадийном механизме изменения энтропии системы в элементарных реакциях разрыва (рекомбинации межмолекулярных и химических связей в газовой фазе, протекающих через образование переходного состояния. Приведены результаты оценок энтропий слипания молекул по энтропиям сжатия системы в ходе образования молекулярных комплексов с последующим расчетом их энтропий образования с помощью известных стандартных энтропий образования исходных молекул.

MATHEMATICAL MODELS FOR FORMATION ENTHROPYS MOLECULAR INTERMADIARY STATES AND INTERMADIARY MOLECULAR COMPLEXES VALUE FROM INITIAL MOLECULAS FORMATION ENTHROPYS IN GASEOUS PHASE

Dudorov V.V., Melchakova T.A., Gurbatova A.P.

(Nizhnii Novgorod)

Two stages mechanism of system entropy change at gaseous elementary reactions of dissociation (recombination) intermolecular and chemical bonds, flowing through intermediate state formation have been putted to obtain purposeful mathematical models. Molecular condensation enthropy values results from compression of system in molecular complexes formation process have been to utilize at formation enthropys these complexes to the assistance of known standard formation enthropys for initial molecules.

По современным представлениям процессы образования лабильных переходных структур, активированных переходных состояний (комплексов), и промежуточных молекулярных комплексов выполняют важные функции в кинетике и механизме химических реакций. С образованием активированных состояний обычно связывают протекание элементарных реакций (стадий), тогда как с образованием промежуточных молекулярных комплексов – механизмы большинства сложных реакций. Энтропии образования как активированных, так и молекулярных комплексов, как правило, неизвестны. Достаточно точный расчет этих величин методами статистической термодинамики затруднителен вследствие отсутствия достоверных сведений о геометрической структуре и энергиях связи в подобных образованиях.

Нами предлагается методика оценки энтропий образования активированных и молекулярных комплексов в газовой фазе по данным о термодинамических энтропиях образования исходных реагентов и энтропиях сжатия системы в процессах образования таких комплексов. Основу методики составляет развиваемое нами представление [1] о двухстадийном механизме изменения энтропии системы в элементарных реакциях разрыва ( рекомбинации) межмолеклярных и химических связей в газовой фазе. Этот механизм хорошо согласуется со схемой протекания обратимой элементарной реакции, принимаемой [2] в теории переходного состояния (активированного комплекса), когда схема равновесия X « Y между исходными и конечными веществами может быть записана в виде

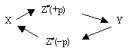⁽¹⁾

где Z^¹ - промежуточный комплекс, символы +р и -p указывают, что в направлении прямой реакции количество движения промежуточного комплекса имеет положительный знак, а в направлении обратной реакции - отрицательный при одинаковом химическом составе и геометрической структуре комплекса.

В двухстадийном механизме изменения энтропии системы при разрыве (рекомбинации) межмолекулярной или химической связи в газовой фазе существенна только энтропия активации образования переходного состояния реакции, так как вторая стадия его разрушения (стабилизации), по-видимому, протекает самопроизвольно. Последнее свидетельствует о реальности существования переходного состояния (активированного комплекса) в обратимой элементарной химической реакции как некоторой пространственно-энергетической структуры, для образования которой как в направлении прямой, так и в направлении обратной реакции необходимы одинаковые по абсолютной величине приращения энтропии системы, равные половине абсолютного значения собственно энтропии реакции. Последнему соответствует справедливость равенств:= -= -DS⁰/2, где DS⁰ - приращение энтропии в реакции диссоциации связи при стандартных условиях, а и - соответственно в прямой и обратной стадиях образования переходного состояния (комплекса) по схеме (1). В результате изменение энтропии макросистемы в реакции диссоциации (рекомбинации ) связи А-В можно описать системой уравнений:

+ S⁰_AB =

+ S⁰_А+ S⁰_B = (2)

+= 0

где или – стандартная энтропия образования активированного комплекса.

Решения системы (2) имеют вид:

= = (S⁰_A + S⁰_B + S⁰_AB ) ¤ 2 (3)

D = (S⁰_A + S⁰_B - S⁰_AB ) ¤ 2 (4)

= (S⁰_AB - S⁰_A - S⁰_B) ¤ 2 (5)

По формуле (3) можно рассчитать энтропию образования активированного комплекса, а по формулам (4) и (5) – соответственно энтропии активации прямой и обратной реакций с помощью известных значений стандартных энтропий образования исходных и конечных реагентов. С другой стороны, формула (5) может быть использована для расчета неизвестной стандартной энтропии образования промежуточного молекулярного комплекса в рамках элементарной обратимой бимолекулярной реакции: А + В = А×В:

S⁰_A×B = 2+ S⁰_A + S⁰_B (6)

где , как ранее нами было показано [1], численно равна стандартной энтропии сжатия системы при образовании переходного состояния (активированного комплекса) в реакции.

Наиболее простой задачей является определение энтропии образования молекулярного комплекса из молекул одного и того же вещества, если энтропию сжатия при его образовании в первом приближении принять равной энтропии сжатия системы при фазовом переходе пар-жидкость для этого вещества.

В качестве стандартной энтропии сжатия индивидуального вещества при фазовом переходе пар – жидкость допустимо принять величину:

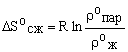(7)

где r⁰_ж, r⁰_пар - плотности жидкости и пара при температуре, достаточно близкой к нормальной температуре кипения (Т_к) при давлении насыщенного пара, равном стандартному значению. В случае отсутствия справочных данных о величинах r⁰_ж и r⁰_пар для оценки величины можно использовать формулу:

(8)

где величина r_ж равна плотности жидкости при 20⁰С, а плотность пара рассчитывается с помощью уравнения Менделеева-Клапейрона. Нетрудно убедиться, что для достаточно исследованных жидкостей относительное превышение величины (8) над (7) невелико. Для воды - не более 0,8%, для н-гексана - не более 2,2%, а для циановодорода величина (8) даже меньше (7) на 2,8%, что в совокупности свидетельствует о возможности применения формулы (8). В последней величину r_ж также допустимо заменить на r⁰_ж, которая для многих низкокипящих веществ известна. Нетрудно убедиться, что при этом в случае наиболее исследованных веществ разница в результатах расчетов по указанным формулам невелика. Для гелия - не более 17%, для азота - 0,02%, для кислорода - 0,3%, для этилена - 0,4%, для пропана - 1,5%, для н-гексана - 0,5%.

Процесс образования молекулярного комплекса типа А×В, при слипании отличных по свойствам молекул, имеет много общего, но, конечно, не является копией фазового перехода пар – жидкость, поэтому определение соответствующей энтропии сжатия непростая задача. За отсутствием методов оценки подобной величины её, в первом приближении, можно принять равной полусумме энтропий сжатия в процессах конденсации индивидуальных парообразных реагентов А и В соответственно. Полученная таким образом величина приобретает смысл изменения энтропии системы в результате исчезновения одного моля газообразного вещества за счет слипания частиц А и В. Однако, процесс слипания в большинстве случаев является сложным и может протекать, по крайней мере, в две элементарные стадии:

k₁ k₂

А + В ^« (А×В)* ; (А×В)* ® А×В

k_-1

где (А×В)* – нестабилизированный молекулярный комплекс (квазимолекула), подвергающийся стабилизации, и макроскопическая константа скорости в приближении стационарности концентрации (А×В)* описывается формулой:

k = k₁×k₂ /(k_-1 + k₂ ) (9)

где константа k₂ представляет собой сумму констант скоростей стабилизации квазимолекулы по трем возможным механизмам: внутримолекулярному, радиационному и ударному при столкновении (А×В)* с третьей частицей М (k₂ = k[M]).

Зависимость (9) позволяет применить схему (1) к процессу образования комплекса А×В в двух крайних случаях: k_-1 << k₂ (лимитирующая стадия процесса – элементарная реакция образования (А×В)*, и k = k₂ ) либо k_-1 >> k₂ (лимитирующая стадия – процесс стабилизации (А×В)*, и k = k₁×k₂ /k_-1 , т.е. представляет собой сложную константу). . В случае преимущественно ударной стабилизации при условии k_-1 >> k[M] меняется лишь кинетический закон протекания реакции от второго к третьему.

В случае неравенства k_-1 << k₂ допустимо принять, что состояние нестабилизированного комплекса идентично переходному состоянию системы при образовании молекулярного комплекса А×В. Это делает уравнение (6) справедливым для оценки энтропии образования комплекса А×В.

В случае противоположного неравенства k_-1 >> k₂ допустимо принять,что отношение k₁ /k_-1 – константа равновесия, и для оценки изменения энтропии системы воспользоваться системой уравнений:

DS_(«) + S⁰_А+ S⁰_B = S⁰_(A×B)*

+ S⁰_(A×B)* + S⁰_М = + S⁰_М (10)

+ S⁰_А×В + S⁰_М = + S⁰_М

где DS_(«) – изменение энтропии системы при образования нестабилизированного комплекса (А×В)*, или энтропии образования переходного состояния в ходе стабилизации (дестабилизации) (А×В)*.

В результате сложения правых и левых частей двух верхних и вычитания нижнего уравнения системы (10) нетрудно получить соотношение, отличающееся от (6) только числом слагаемых в сумме: DS_(«) + -, характеризующей суммарное изменение энтропии системы при образовании комплекса А×В. Последнее допускает использование выражения (6) для оценки величины энтропии образования молекулярного комплекса типа А×В и в области k_-1 >> k_2, что не противоречит известному положению о том, что изменение энтропии в обратимой реакции является полным дифференциалом и не зависит от механизма протекания реакции.

Таблица 1. Энтропии слипания молекул в газовой фазе.

№	Акт слипания А + М = А×М	r^0пар(М), г×л^-1	r^0ж(М), г×см^-3	DSсж(М),	DSсл (М),
				Дж×моль^-1 К^-1
1	С2Н6 + С2Н6 = С2Н6×С2Н6	1,357	0,5612	–50,08	–100,16
2	С2Н6 + Ne = С2Н6×Ne	0,90035	1,204	–55,43	–105,51
3	С2Н6 + H2 = С2Н6×H2	0,08988	0,0708	–33,88	-83,96
4	H2 + H2 = H2×H2	0,08988	0,0708	-33,88	-67,76
5	H2 + H2О = H2×H2О	0,5977	0,95838	-58,87	-92,75
6	H2О + Hе = H2О×Hе	0,01672	0,12517	-17,01	-75,88
7	О2 + О2 = О2×О2	4,408	0,1140	-46,18	-92,36
8	Br2 + Br2 = Br2×Br2	5,872	3,1023	-52,11	-104,22
9	H2 + Ar = H2×Ar	1,7831	1,40	-55,35	-89,23
10	H2O+ Ar = H2O×Ar	1,7831	1,40	-55,35	-110,98
11	O2 + Ar = O2×Ar	1,7831	1,40	-55,35	-101,53
12	Br2 + Ar = Br2×Ar	1,7831	1,40	-55,35	-107,46
13	H2O+ Xe = H2O×Xe	5,857	3,52	-53,18	-112,85
14	O2 + Xe = O2×Xe	5,857	3,52	-53,18	-99,38

Таблица 2. Энтропии образования молекулярных комплексов в газовой фазе

№	Акт слипания А + М = А×М	S^0пост(А×М),	S^0(А×М),	Доля вклада S^0пост(А×М),%
			Дж×моль^-1×К^-1
1	С2Н6 + С2Н6 = С2Н6×С2Н6	159,68	358,82	45,3
2	С2Н6 + Ne = С2Н6×Ne	157,13	269,47	58,3
3	С2Н6 + H2 = С2Н6×H2	148,95	275,40	54,1
4	H2 + H2 = H2×H2	126,03	193,38	65,2
5	H2 + H2О = H2× H2О	155,45	226,54	68,6
6	H2О + Hе = H2О×Hе	145,97	238,88	61,1
7	О2 + О2 = О2×О2	160,43	317,67	50,5
8	Br2 + Br2 = Br2×Br2	180,45	386,48	46,7
9	H2 + Ar = H2×Ar	155,16	196,07	78,7
10	H2O+ Ar = H2O×Ar	159,22	229,24	69,5
11	O2 + Ar = O2×Ar	161,89	261,46	61,9
12	Br2 + Ar = Br2×Ar	174,60	292,62	59,7
13	H2O+ Xe = H2O×Xe	171,00	245,45	69,7
14	O2 + Xe = O2×Xe	172,09	275,23	62,5

Результаты расчета стандартных энтропий слипания молекул некоторых веществ приведены в табл.1. Полученные значения в дальнейшем были использованы для уточнения оценок констант скоростей разрыва и рекомбинации химических связей в газовой фазе, приведенных в работах [4,5]. О степени достоверности полученных данных можно судить по результатам сравнения в табл.2 рассчитанных по формуле (6) значений энтальпий образования молекулярных комплексов с теоретическими величинами поступательных составляющих энтропий их образования, вычисленных для стандартных условий (Т=298,15 К, Р=1.01×10⁵ Па) по известной методике [6]. Из сравнения следует, что ожидаемый вклад вращательных и колебательных составляющих энтропии образования особенно велик в случае молекулярных комплексов, образованных многоатомными или тяжелыми молекулами с преимущественно большими моментами инерции. Последнее не противоречит общепринятым представлениям.

При получении изложенных результатов были использованы справочные данные из источников [7-14].

Список литературы:

1.Дудоров В.В., Мельчакова Т.А.// Сб. Математика. Компьютер. Образование. М. Вып.8. Ч.2. 2001. С.

2.Кондратьев В.Н. Кинетика химических газовых реакций. М., 1958. С.197-216.

3.3. Кондратьев В.Н., Никитин Е.Е. Кинетика и механизм газофазных реакций. М., 1974. С.242-254.

4.Дудоров В.В., Мельчакова Т.А. //Сб. Математика. Компьютер. Образование. М. Вып.6. Ч.2. 1999. С. 380 - 385.

5.Дудоров В.В., Мельчакова Т.А., Мишанов А.Р. // Сб. Математика. Компьютер. Образование. М.: Вып.7. Ч.2. 2000. С.644-651.

6.Левич В.Г. Введение в статистическую физику. М., 1954. С.230-240.

7.Справочник химика. М. -Л. Т.1.1963.

8.Краткий справочник по химии. Киев. 1974.

9.Термодинамические свойства гелия. М. 1984.

10.Термодинамические свойства азота. М. 1977.

11.Термодинамические свойства кислорода. М. 1981.

12.Термодинамические свойства этилена. М. 1981.

13.Термодинамические свойства пропана. М. 1989.

14.Термодинамические свойства н-гексана. М. 1990.