МАТЕМАТИКА И ТЕРМОДИНАМИЧЕСКАЯ ЭНТРОПИЯ

Дудоров В.В., Мельчакова Т.А.

(Нижний Новгород)

В соответствии с математическим описанием, опирающимся на экспериментальные данные, изменение энтропии системы при разрыве межмолекулярных связей в процессах кипения жидкостей или химических связей в газообразных молекулах состоит из двух равных частей: энтропии активации образования переходной пространственно-энергетической структуры (состояния) и энтропии последующего самопроизвольного расширения ее до образования дополнительного числа молей газообразного вещества.

MATHEMATICS AND THERMODYNAMIC ENTROPY

Dudorov V.V., Melchakova T.A.

(Nizhnii Novgorod)

In accordance with the mathematical description, leaning on experimental data, system entropy changing at molecular bonds break — up under liquid boiling or at chemical bonds break in gaseous molecules consists of two equal parts: entropy to activations of forming transition space-energy structure (condition) and entropy of folloing spontaneous expansion it before forming on additional number of moles of gaseous material.

Все этапы развития понятия термодинамической энтропии тесно связаны с теоретической математической интерпретацией ее физико-химического смысла. Понятие энтропии было введено в науку в 1865 г. немецким физиком-теоретиком Р. Клаузиусом чисто математически в качестве меры необратимого рассеяния энергии в процессах теплопередачи [1]. Экспериментальная трактовка энтропии впервые была получена в рамках теоретического уравнения Клаузиуса — Клапейрона, составившего основу теоретического объяснения эмпирического правила Трутона для фазового перехода жидкость–пар. Далее российским физико-химиком Н. Кобозевым [2] математическим путем было показано, что приращение энтропии системы, обусловленное изменением числа молей газообразных веществ в химических реакциях, также близко к величинам, удовлетворяющим правилу Трутона.

Теоретическая интерпретация энтропии на молекулярно-кинетическом уровне была дана в 1872 г. австрийским физиком Л. Больцманом, математически связавшим энтропию с вероятностью состояния физико-химической макросистемы, что вместе с третьим началом термодинамики, сформулированным в 1906 г. немецким физиком и физико-химиком В. Нернстом, легло в основу теоретического расчета энтропии индивидуальных газообразных веществ методами статистической термодинамики.

При разработке методики расчета констант скоростей реакций диссоциации и рекомбинации химических связей в газовой фазе по стандартным значениям термодинамических функций исходных и конечных реагентов нами было обнаружено, что энтропия активации превращения составляет не более половины собственно энтропии реакции [3]. Этот удивительный факт потребовал дополнительных исследований механизма изменения энтропии в ходе превращения. Перед изложением результатов исследований целесообразно указать место, которое занимает предлагаемая нами методика среди уже известных методов расчета констант скоростей химических газовых реакций.

В настоящее время при расчете констант скоростей элементарных реакций применяются методики [4-7], основанные на двух принципиальных подходах: а) расчет на основе молекулярно-кинетической теории соударений в рамках статистической теории Райса-Рамспергера-Касселя-Маркуса (РРКМ) и б) расчет по методу переходного состояния (активированного комплекса) в рамках теории абсолютных скоростей реакций Вигнера-Поляни-Эйринга-Эванса. Оба подхода опираются на представления об активированном комплексе и на достаточно подтверждающиеся предположения. Первое допускает монотонное адиабатическое движение ядер взаимодействующих атомов без электронных переходов со скачкообразным изменением потенциальной энергии системы, согласно второму движение ядер может быть описано законами классической механики, согласно третьему химическая реакция не нарушает максвелл-больцмановское распределение реагирующих молекул по энергиям.

Мономолекулярную реакцию диссоциации химической связи в случае термической активации принято описывать схемой Линдемана из двух элементарных реакций: бимолекулярной и мономолекулярной:

k_a k*

А₂ + М ^« А₂* + М ; А₂* ® А₂^¹ ® А + А (1)

k_-a

где А₂* — активная, A₂^{¹ —} активированная молекула, подвергающаяся превращению.

В первом из подходов для получения значений констант k_a и k_-a необходимо решение двух достаточно сложных задач: а) динамической, связанной с расчетом поперечного сечения соударения и б) статистической, связанной с расчетом функций распределения участвующих в соударении молекул по энергиям, причем вид этих функций в механизмах сильных и слабых столкновений различен. Для получения значений константы k* решается задача, связанная с выбором механизма внутримолекулярного перераспределения энергии. Главными источниками погрешностей расчета являются неопределенности исходных данных о виде функций распределения, числе состояний активированного комплекса и механизме внутримолекулярного перераспределения энергии.

Во втором подходе решение динамической задачи заменяется решением статической задачи путем использования представления о многомерной поверхности потенциальной энергии системы, являющейся функцией потенциальной энергии ядер и внутренних координат (степеней свободы) реагирующих молекул. Химическая реакция рассматривается как переход из конфигурации реагентов в конфигурацию продуктов через конфигурацию седловой точки (активированного комплекса) вдоль координаты реакции, и скорость реакции определяется свойствами этой геометрической конфигурации химической системы. Затем предполагается, что величина константы скорости необратимой реакции мало отличается от значения константы при наличии химического равновесия, допускается осуществление термодинамического равновесия между активированным комплексом и исходными или конечными продуктами, и схема равновесия X«Y между исходными и конечными веществами записывается в виде:

Z^¹(+p)

X Y (2)

Z^¹(-p)

где Z^¹ — промежуточный комплекс, символы +р и -p указывают, что в направлении прямой реакции количество движения промежуточного комплекса имеет положительный знак, а в направлении обратной реакции — отрицательный при одинаковом химическом составе и геометрической структуре комплекса. На основании такого допущения константы скоростей прямой и обратной реакций описываются уравнениями:

₍₃₎

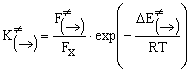
₍₄₎

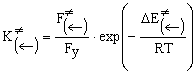
где F^¹ _(®), F^¹_(¬) и F_x, F_y — отнесенные к единице объема статистические суммы по состояниям активированного комплекса и реагентов; а DE _(®) и DE _(¬) — изменения внутренней энергии при перемещении химической системы по поверхности потенциальной энергии реакции, построение которой в этом методе необходимо для определения истинного характера зависимости энергии системы от расположения взаимодействующих атомов, т.е. для оценки DE^¹_(®) либо DE^¹_(¬). Неопределенности исходных данных при построения поверхности потенциальной энергии являются главными источниками погрешностей для определения конфигурации активированного комплекса и его характеристик. Допустив, что величины K^¹ _(®) и K^¹_(¬) являются константами равновесия, выражения (3) и (4) можно представить в термодинамической форме записи:

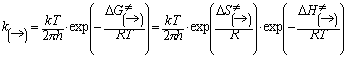(5)

а для константы скорости обратной реакции:

(6)

Результат деления правой и левой частей уравнения (5) соответственно на правую и левую части уравнения (6) представляет собой константу химического равновесия реакции X «Y.

Предлагаемая нами методика основывается на использовании изотермы химической реакции, приведенной к стандартному состоянию по внутренним параметрам системы:

lnK_p = -DG⁰/RT (7)

в рамках расчета констант скоростей по методу переходного состояния (активированного комплекса].

В расчете константы скорости мономолекулярной реакции диссоциации с помощью соотношения (5) величина принималась равной энтальпии разрыва (DH⁰) связи А–В при стандартных условиях (T⁰=298 К), а величина для обратной реакции бимолекулярной рекомбинации в соотношении (6) — равной работе сжатия –RT⁰. Для оценки величин и при условии их совпадения с соответствующими стандартными значениями подвергали анализу возможные решения системы уравнений:

+ S⁰_А+ S⁰_B =

+ S⁰_AB = (8)

^{-----------------------------------------------}

-= DS⁰ = S⁰_A + S⁰_B - S⁰_AB

где DS⁰ — приращение энтропии реакции диссоциации, или — стандартная энтропия образования промежуточного комплекса.

Система (8) не имеет однозначного решения, поскольку её определитель равен нулю. Однако, методом последовательных приближений при условии выполнения требования =можно доказать справедливость равенств:= -= -DS⁰/2, откуда следует, что при DS⁰ > 0, величина >0, а <0. Таким выводам удовлетворяют и решения системы (8), дополненной третьим уравнением: + = 0. Это позволило в области давлений, где реакция диссоциации протекает по закону первого, а реакция рекомбинации — по закону второго порядка, представить расчетные выражения для констант скоростей в виде:

k_d = c_d ×× exp(DS⁰/2R)×exp(-DH⁰/RT) (9)

k_r = c_r ×× (RT)×exp(-DS⁰/2R)×exp(T⁰/T) (10)

где c — коэффициент прохождения через конфигурацию активированного комплекса.

Формула (9) была использована, в частности, для расчета элементарной константы скорости бимолекулярной рекомбинации этильных радикалов при Т=298К. Значение 12,65 для десятичного логарифма константы скорости, выраженной в см³×моль^-1×с^-1, оказалось близким к эмпирическим и расчетным величинам, определенным другими методами [8].

Полученные результаты могли свидетельствовать о реальности существования переходного состояния (активированного комплекса) в обратимой химической реакции как некоторой пространственно-энергетической структуры, для образования которой как в направлении прямой, так и в направлении обратной реакции необходимы одинаковые по абсолютной величине приращения энтропии системы, равные половине абсолютного значения собственно энтропии реакции. Однако, достоверность этого желательно было подтвердить экспериментальными данными. Наиболее подходящими для этого являются достаточно обширные сведения о процессах испарения и кипения жидкостей, которые можно интерпретировать в рамках гетерогенной реакции, если используемое обычно уравнение Клаузиуса-Клапейрона заменить выражением (7) и для описания константы скорости испарения воспользоваться выражением типа (5), а для описания константы скорости конденсации выражением типа (6). В этом случае можно было ожидать, что приращение энтропии при образовании переходного состояния в направлении конденсации пара в жидкость будет равно половине собственно энтропии конденсации жидкости. Допустив, что эта часть полного приращения энтропии равна энтропии сжатия при конденсации паров в жидкость при температуре кипения, нетрудно было оценить ее величину по справочным данным.

В качестве стандартного значения энтропии конденсации принимали величину разности между стандартными величинами энтропий образования жидкого и газообразного состояний веществ. Для расчета стандартной энтропии сжатия использовали формулу:

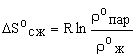(11)

где r⁰_ж, r⁰_пар — плотности жидкости и пара при температуре, достаточно близкой к нормальной температуре кипения (Т_к) при давлении насыщенного пара, равном стандартному значению. В случае отсутствия справочных данных о величинах r⁰_ж и r⁰_пар для оценки величины использовали формулу:

(12)

где величина r_ж обычно была равна плотности жидкости при 20⁰С, а плотность пара рассчитывалась на основании уравнения Менделеева-Клапейрона. Нетрудно убедиться, что в случае достаточно исследованных жидкостей относительное превышение величины (12) над (11) невелико. Для воды — не более 0,8%, для н-гексана — не более 2,2%, а для циановодорода величина (12) даже меньше (11) на 2,8%, что в совокупности свидетельствует о возможности применения формулы (12).

Сравнение стандартных энтропий расширения с величинами стандартных энтропий фазового перехода жидкость — пар произведено в табл.1 по результатам расчетов для 22 веществ, имеющих справочные значения стандартных энтропий образования в жидком и газообразном состояниях. Из результатов статистической обработки по всем веществам следует, что величина отношения сопоставленных величин при доверительной вероятности 0,95 колеблется около значения 2,07 ± 0,10. Отклонения от этого значения, в случае отдельных веществ, превышающие указанную погрешность, допустимо объяснить наличием погрешностей в использованных исходных справочных данных и, в значительной степени, идеализированными моделями расчета величин (11) и (12), не учитывающими возможных эффектов ассоциации молекул в жидкостях и парах. Таким образом, данные из табл.1 в целом не противоречат выводам, следующим из решения системы (8), позволяя заключить, что стандартная энтропия активации разрыва (образования) межмолекулярной или химической связи действительно может быть численно равна стандартной энтропии расширения (сжатия) системы в соответствующем процессе. Это открывает возможность расчета стандартных энтропий активации и энтропий фазовых переходов жидкость–пар по величинам стандартных энтропий расширения (сжатия) системы и для веществ, температура кипения которых далека от 298К. Могут быть использованы формулы (11) и (12), если в последней величину r_ж заменить на r⁰_ж, которая для многих низкокипящих веществ известна. Нетрудно убедиться, что при этом в случае наиболее исследованных веществ разница в результатах расчетов по указанным формулам невелика. Для гелия — не более 17%, для азота — 0,02%, для кислорода — 0,3%, для этилена — 0,4%, для пропана — 1,5%, для н-гексана — 0,5%.

Из результатов расчетов, приведенных в табл. 1 следует также, что величина стандартной энтропии образования моля газообразного вещества при разрыве химической связи в газовой фазе должна совпадать со стандартной энтропией разрыва этой связи, тогда как при фазовом переходе жидкость–пар — со стандартной энтропией подобного перехода. Совокупность полученных данных не противоречит схеме равновесия (2) и позволяет интерпретировать изменение энтропии системы при разрыве (образовании)межмолекулярных и химических связей в рамках двухстадийного механизма, где существенна только энтропия активации первой стадии, так как вторая стадия, по-видимому, протекает самопроизвольно. Такому механизму удачно соответствует греческое понимание энтропии как превращения или поворота.

Двухстадийный механизм изменения энтропии системы при разрыве (образовании) межмолекулярных и химических связей позволяет объяснить необратимое рассеяние энергии в процессах теплопередачи образованием и разрушением квазимолекул при неупругих соударениях в макросистеме. Потеря энергии может происходить на стадиях как радиационной стабилизации, так и столкновительного разрушения квазимолекул, то есть на стадиях разрушения и образования пространственно-энергетических переходных структур (состояний).

Образование и разрушение пространственно-энергетической переходной структуры можно интерпретировать с физико-химической точки зрения соответственно как появление в веществе или выделение из вещества пространственной дырки, обладающей определенной энергией. Дырка, соответствующая энтропии активации разрыва связи, является носителем пространства в веществе, трансформирующимся в момент разрыва связи в носителя одного из продуктов разрыва в виде некоторого эффективного объема окружающего пространства. При рекомбинации связи процесс, скорее всего, протекает в обратном направлении. Не исключено, что при стабилизации квазимолекулы выделение дырки из вещества может происходить не только по столкновительному, но и по радиационному механизму.

Вышеизложенное свидетельствует о приоритетности вклада математических описаний (моделей) для понимания физико-химического смысла термодинамической энтропии системы при определении меры рассеяния энергии в процессах теплопередачи.

При получении изложенных результатов были использованы справочные данные из источников [9-15].

Таблица 1. Взаимосвязь стандартной энтропии фазового перехода жидкость – пар с энтропией расширения системы.

№	Вещество	S^0(г)- S^0(ж), Дж×К^-1×моль^-1	-DS^0сж, Дж×К^-1×моль^-1	[S^0(г)- S^0(ж)] ^_________ (-DS^0сж)	-DS¢сж, Дж×К^-1×моль^-1	[S^0(г)- S^0(ж)] ^_________ (-DS¢сж)
1	Вода	118,53	61,34	1,93	61,80	1,92
2	Тяжелая вода	122,23			63,33	1,93
3	Метанол	110,90			54,27	2,04
4	Муравьиная кислота	122,05			55,69	2,19
5	Этанол	121,3			51,55	2,35
6	Ацетон	95,8			49,11	1,95
7	Изопропанол	126,7			49,43	2,56
8	Уксусная кислота	133,5			52,54	2,54
9	Циклопентан	88,62			46,85	1,89
10	Сероуглерод	86,82			42,26	2,05
11	Бензол	96,40			48,09	2,00
12	н-Гексан	92,51	43,67	2,12	44,63	2,07
13	Толуол	100,16			52,46	1,91
14	п-Ксилол	105,06			46,64	2,25
15	о-Ксилол	106,27			46,98	2,26
16	м-Ксилол	105,52			46,70	2,26
17	н-Гептан	99,24			44,36	2,24
18	Хлороформ	93,58			48,55	1,93
19	Тетрахлорид углерода	94,98			47,34	2,01
20	Бром	93,03			52,12	1,78
21	Тетрахлорид кремния	92,04			45,44	2,03
22	Ртуть	98,75			67,80	1,46

Список литературы:

1. Зубарев Д.Н. //Физика.-М.:Большая Российская энциклопедия, 1999.С. 903-905.

2. Кобозев Н.И. //Ж.физ.химии. 1948. Т.22. №8. С 1002-1015.

3. Дудоров В.В., Мельчакова Т.А. //Сб. Математика. Компьютер. Образование. М. Вып.6. Ч.2. 1999. С. 380-385.

4. Кондратьев В.Н. Кинетика химических газовых реакций. М. 1958. С. 291.

5. Кузнецов Н.М. //Химическая энциклопедия. М. Т.1. 1988. С. 257-260.

6. Кондратьев В.Н., Никитин Е.Е. Кинетика и механизм газофазных реакций М. 1974. С. 85.

7. Базилевский М.В. //Химическая энциклопедия. М. Т.1. 1988. С. 121-125.

8. Дудоров В.В., Мельчакова Т.А., Мишанов А.Р. // Сб. Математика. Компьютер. Образование. М.: Вып.7. Ч.2. 2000. С.

9. Краткий справочник по химии. Киев. 1974.

10.Термодинамические свойства гелия. М. 1984.

11.Термодинамические свойства азота. М. 1977.

12.Термодинамические свойства кислорода. М. 1981.

13.Термодинамические свойства этилена. М. 1981.

14.Термодинамические свойства пропана. М. 1989.

15.Термодинамические свойства н-гексана. М. 1990.