КИНЕТИКА КЛЕТОЧНЫХ ПОПУЛЯЦИЙ

В ЭКОТОКСИКОЛОГИЧЕСКИХ МОДЕЛЯХ

Ершов Ю.А., Котин В.В.

(Москва)

Детерминированные и стохастические задачи динамики популяций неоднократно рассматривались ранее [1, 3, 4] и традиционны для математической экологии. Вместе с тем интерес к этим задачам, особенно стохастическим, постоянно возобновляется [5-7]. В настоящей работе исследуются экотоксикологические модели, описывающие воздействие химических агентов на рост клеток [12, 13].

1. Детерминированная экотоксикологическая модель.

Уравнения экотоксикологической детерминированной модели в нормированном виде записываются следующим образом [12]:

(1)
где

(2)

Здесь z₁, z_{2 –} населенности двух групп клеток, нормированные на емкость b/a среды без воздействия токсикантов: z₁=c₁a/b, z₂=c_ma/b, t=pt – безразмерное время,

c₁, c_m – населенности групп растущих и митотических клеток; a,b,p -кинетические коэффициенты автоингибирования, рождения (разветвления), и роста популяционной цепи, w_{1 –} мощность внешнего источника клеток с₁, f – коэффициент размножения. Коэффициенты b₁ и p₁ являются функциями от концентрации ингибиторов x₁ и x₂:

p_x=p+d₁; b_x = b + d₂ , d₁ = d₁₁ x₁ + d₁₂ x₂; d₂ = d₂₁ x₁ + d₂₂ x₂ .

Известно, что разделение характерных временных масштабов в задачах биокинетики позволяет упростить анализ и выявить существенные особенности взаимосвязанных процессов [3]. Соотношение характерных времен двухстадийного роста клеток первой z₁ и второй z₂ группы зависит от параметра m=b/p. Если константы скорости рождения b и продолжения цепи p соотносятся таким образом, что m>>1, то полная система (1) редуцируется к вырожденному (медленному) уравнению:

, (3)

где

Эффект ингибирования – уменьшение стационарного значения населенности z_st -эквивалентен снижению эффективной емкости среды при наличии токсикантов. Найдем диапазон концентраций токсикантов, при которых стационарная населенность двухуровневой популяции z_st(х₁,х₂) не меньше заданной величины sі0. Множество значений концентраций токсикантов {х₁,х₂}, удовлетворяющих этому условию, определяется неравенством

(4)
где

В плоскости (х₁,х₂) условие (4) задает область {0Јx₁Јx₁^*, 0Јx₂ЈF(x₁,s)}, в пределах которой концентрация токсикантов такова, что рост популяции возможен. Нулевому уровню стационарной населенности s=0 в плоскости параметров (х₁,х₂) соответствует критическая кривая биоцидного действия z_st(х₁,х₂)=0, задающая верхнюю границу области роста G. Если концентрации токсикантов превышают критический уровень, определяемый границей s=0, то рост популяции полностью подавляется. Рис.1 демонстрирует зависимость стационарной населенности z_st(х₁,х₂) от концентрации токсикантов для популяции без источников (W=0). Кривые постоянного уровня населенности и критическая кривая биоцидного действия z_st(х₁,х₂)=0 показаны на рис.2а.

В системе без источников (W=0) нулевой уровень z_st(х₁,х₂)=0 является бифуркационной кривой, на которой перестраивается фазовый портрет. Критическая кривая биоцидного действия ВС разбивает плоскость параметров (х₁,х₂) на области G и R (рис. 2а). В области G плоскости параметров (х₁,х₂) существует две особых точки – седло (0,0) и устойчивый узел (z*₁,z*₂). В области R плоскости параметров (х₁,х₂) существует единственная особая точка – устойчивый узел (0,0). На критической кривой ВС устойчивый узел (z*₁,z*₂) сливается с седлом (0,0), образуя множественную особую точку седло-узел, которая при дальнейшем росте концентрации токсикантов и переходе в область R трансформируется в устойчивый узел. Фазовые портреты системы в областях R и G пространства параметров (х₁,х₂) показаны на Рис. 2б. Математический анализ детерминированной экотоксикологической модели и графическое представление фазовых траекторий реализованы с использованием пакета MAPLE V R5 [14].

Рис. 1. Стационарная населенность z_st в зависимости от концентрации токсикантов для изолированной популяции (при отсутствии внешнего потока клеточной массы W=0). Показаны кривые постоянного уровня стационарной численности популяции z_st(х₁,х₂)=const. Нулевой уровень z_st(х₁,х₂)=0 соответствует критической кривой биоцидного действия.

а) б)

Рис.2. (а) Бифуркация на критической кривой биоцидного действия BС. В области G две особых точки – седло (0,0) и устойчивый узел (z^st₁, z^st₂). В области R единственная особая точка- устойчивый узел. На BС – множественная особая точка седло-узел (0,0). (б) Фазовые портреты системы в области R при х₁₌2, х₂₌5, p/b=0.1 и в области G, p/b=0.02.

2. Стохастическая динамика клеточных популяций и время жизни.

Клеточную популяцию в среде со случайными возмущениями рассмотрим как нелинейную динамическую систему с флуктуациями [2, 5-7]. Приемлемой моделью быстрых флуктуаций обычно является стационарный дельта-коррелированный случайный процесс (белый шум). Выделим два типа возмущений. Первый тип- аддитивные шумы (флуктуации мощности внешнего источника dW). Второй тип– параметрические шумы (случайные изменения кинетических коэффициентов), приводящие к появлению в уравнениях стохастической динамики мультипликативных членов, зависящих от состояния системы в данный момент времени [5].

Математическое ожидание времени первого достижения заданных границ z_min, z_max находится из решения краевой задачи [2, 6, 13]:

, z_min<z<z_max (5)
T(z_min)=0; T(z_max)=0, a(z) и b(z) – коэффициенты сноса и диффузии в уравнении Фоккера-Планка-Колмогорова.

Выбор нижней границы z_min=0 (или z_min=z_В, где z_В–нижний порог численности, по достижении которого популяция вырождается) соответствует условию гибели популяции. Верхняя граница z_max задается исходя из ограничений ресурсов среды.

Интегральное описание вероятностных темпоральных характеристик системы, эволюционирующей в случайной среде, подразумевает усреднение функции T(z) по начальному распределению численности r(z)

(6)

Такое усреднение учитывает зависимость времени жизни от формы и дисперсии начального распределения r(z), а также от степени близости начального состояния (хвостов начального распределения) к границам жизнеспособности популяции z_min, z_max [13].

Итак, <T> – среднее время существования популяции в пределах ограниченной численности z Н[z_min,z_max], рассматривается как интегральная вероятностная характеристика, определяющая усредненный временной интервал существования популяции в пределах ограниченной численности.

3. Влияние флуктуаций и токсикантов на время жизни популяции.

Исследуем динамику экотоксикологической системы в случайной среде, используя для редуцированной модели аналитический подход, а для анализа двухстадийного роста ингибированной клеточной популяции метод статистического моделирования. В качестве допустимой области существования популяции выделим ограниченный интервал [z_min,z_max]. Случайные возмущения приводят к тому, что изображающая точка M(z) в некоторый случайный момент времени достигает граничных значений z_min, z_max, которые в соответствии с введенным выше определением интерпретируются как допустимые пределы населенности популяции. На Рис. 4,5 представлены результаты численного решения двухточечной краевой задачи (5). При расчетах варьировались координаты граничных точек z_min, z_max, фактор ингибирования l (токсическое воздействие на популяцию) и среднеквадратичная интенсивность случайных возмущений s. Оказывается, что форма начальных распределений весьма незначительно влияет на усредненное время жизни <T>. Основным параметром начального распределения, влияющим на величину <T>, является дисперсия распределения, отнесенная к ширине интервала между границами.

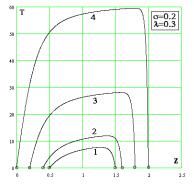
Рис. 4. Время достижения заданного уровня населенности популяции (s=0.2; l=0.3) для различных границ по населенности популяции: 1) zmin=0.5; zmax=1.5; 2) zmin=0.4; zmax=1.6; 3)zmin=0.2; zmax=1.8; 4) zmin=0; zmax=2.

Рис. 5. Время первого достижения заданного уровня населенности популяции для различных значений фактора ингибирования l; zmin=0; zmax=2.

Рис. 6. Случайное блуждание на фазовой плоскости (z₁,z₂) под действием флуктуаций токсичности.

В процессе статистического моделирования двухстадийного роста ингибированной клеточной популяции наряду с аддитивными (внешними) случайными возмущениями в систему вводились также параметрические возмущения, соответствующие вариациям концентрации токсиканта и коэффициента скорости роста клеток. Случайные возмущения моделировались в среде Mathcad 8 [15] посредством различных вариантов программных датчиков случайных чисел (число случайных испытаний N~10⁴ -10⁵).

На Рис. 6 показана реализация случайного процесса блуждания изображающей точки на фазовой плоскости (z₁,z₂) под действием флуктуаций токсичности. Результаты моделирования совместного действия аддитивного и параметрического шума для двух значений мощности внешнего источника W=1, W=2 иллюстрируются на Рис. 7.

Рис. 7. Случайное блуждание на фазовой плоскости (z₁,z₂) при совместном действии флуктуаций токсичности и внешнего источника для двух значений средней величины потока клеточной массы (W=1; W=2).

Выводы.

Действие аддитивных и параметрических шумов делает токсическую границу биоцидного действия в экотоксикологической модели «проницаемой» для нелинейного броуновского блуждания [7] изображающих точек в фазовом пространстве. Существует отличная от нуля вероятность выхода изображающих точек за пределы граничных состояний, даже если детерминированные параметры системы, обеспечивают рост популяции. С другой стороны, если детерминированный рост клеточной массы подавлен токсикантами, но система находится в окрестности критической кривой биоцидного действия, то существует вероятность роста клеточной массы.

Модель описывает популяционную динамику экосистем в условиях токсического действия загрязнений окружающей среды, а также характеристики опухолевого роста с учетом совместного действия цитостатиков, канцерогенов и случайных возмущений.

Литература.

1. Вольтерра В. Математическая теория борьбы за существование. – М., Наука, 1976 .

2. Понтрягин Л.С., Андронов А.А., Витт А.А. ЖЭТФ. – 1933. – Т.3. – Вып.3. – С.165.

3. Романовский Ю.М., Степанова Н.В., Чернавский Д.С. Математическое моделирование в биофизике. – М.: Наука,1975.

4. Свирежев Ю.М. Нелинейные волны, диссипативные структуры и катастрофы в экологии. – М.:Наука, 1987.

5. Хорстхемке В., Лефевр Р. Индуцированные шумом переходы. Теория и применение в физике, химии и биологии. – М.: Мир, 1987.

6. Диментберг М.Ф. Случайные процессы в динамических системах с переменными параметрами. – М.: Наука, 1989.

7. Климонтович Ю.Л. Успехи физических наук. 164 (8). – 1994. – С. 813-842.

8. Ершов Ю.А. Журнал физической химии. – 1998. – Т.72. – №3. – С.553-559.

9. Котин В.В. Тезисы шестой международной конференции «Математика. Компьютер. Образование». – М.: Прогресс-Традиция, 1999. – С. 145.

10. Дьяконов В.П. Математическая система MAPLE V R3/R4/R5. – М.: Солон, 1998.

11. Mathcad User’s Guide. Mathcad 8 Professional Academic. MathSoft, Inc., Cambridge, MA, 1998.